过点D作DE⊥平面ABC，垂足为E，则E是正三角形ABC的中心

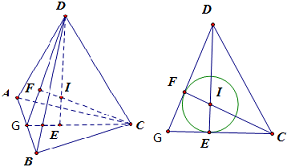
则根据球的对称性和正四面体的性质，得外接球和内切球的球心在同一点处，设为I，则I在高线DE上

延长CE，交AB于G，连接DG，过C作DG边上的高CF，则I在CF上

I到平面ABC的距离IE等于内切球半径r，ID=IC=R是外接球半径

设正四面体棱长为1，则

正△ABC中，CG=

3

2

，CE=

2

3

CG═

3

3

，GE=

1

3

CG=

3

6

，

Rt△DEG中，DG=CG=

3

2

，可得DE=

DG2-GE2

=

6

3

∵Rt△DEG∽Rt△CEI，

∴

EG

EI

=

DE

CE

，即

3

6

：EI=

6

3

：

3

3

，可得EI=

6

12

，所以ID=DE-EI=

6

4

即r=

6

12

，R=

6

4

，

可得

R

r

=1：3，体积比为1：27．

故选C．