问题
解答题
已知抛物线y=x2-2ax+2a+b在x轴上截得的线段长为3,并且此抛物线的顶点坐标满足关系式:y=-x2,求a、b的值。
答案
解:由题意知,抛物线的对称轴为x=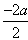 =a
=a
抛物线与x轴交点的横坐标为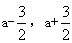
抛物线的解析式也可以写成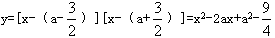
所以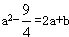 ,令x=a,则y=-
,令x=a,则y=-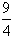 ,所以顶点坐标为
,所以顶点坐标为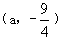
由于顶点坐标满足y=-x2,所以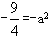
故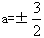
又2a+b=a2-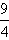 =0
=0
所以b=-2a
所以a=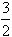 ,b=-3;或a=-
,b=-3;或a=-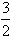 ,b=3。
,b=3。
已知抛物线y=x2-2ax+2a+b在x轴上截得的线段长为3,并且此抛物线的顶点坐标满足关系式:y=-x2,求a、b的值。
解:由题意知,抛物线的对称轴为x=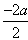 =a
=a
抛物线与x轴交点的横坐标为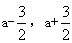
抛物线的解析式也可以写成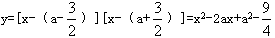
所以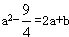 ,令x=a,则y=-
,令x=a,则y=-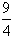 ,所以顶点坐标为
,所以顶点坐标为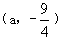
由于顶点坐标满足y=-x2,所以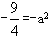
故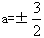
又2a+b=a2-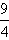 =0
=0
所以b=-2a
所以a=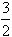 ,b=-3;或a=-
,b=-3;或a=-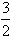 ,b=3。
,b=3。