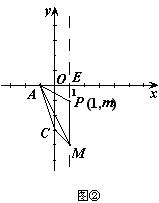问题
解答题
抛物线与x轴交于A(-1,0)、B两点,与y轴交于点C(0,-3),抛物线顶点为M,连接AC并延长AC交抛物线对称轴于点Q,且点Q到x轴的距离为6。
(1)求此抛物线的解析式;
(2)在抛物线上找一点D,使得DC与AC垂直,求出点D的坐标;
(3)抛物线对称轴上是否存在一点P,使得S△PAM=3S△ACM,若存在,求出P点坐标;若不存在,请说明理由。
答案
解:(1)设直线AC的解析式为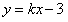 |
把A(-1,0)代入得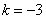 |
∴直线AC的解析式为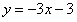 |
| 依题意知,点Q的纵坐标是-6 |
把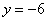 代入 代入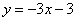 中,解得 ,∴点 Q(1,-6) 中,解得 ,∴点 Q(1,-6) |
∵点Q在抛物线的对称轴上,∴抛物线的对称轴为直线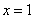 |
设抛物线的解析式为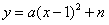 |
由题意,得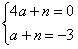 解得 解得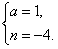 |
∴抛物线的解析式为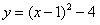 |
| (2)如图①,过点C作AC的垂线交抛物线于点D,交x轴于点N, |
则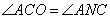 ∴ ∴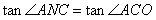 |
∴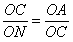 ∵
∵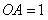 ,
,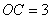 ,∴
,∴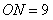
∴点N的坐标为(9,0) 可求得直线CN的解析式为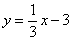
由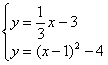 解得
解得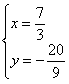 ,即点D的坐标为(
,即点D的坐标为(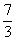 ,
,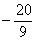 )
)
(3)设抛物线的对称轴交x轴于点E,依题意,得
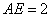 ,
,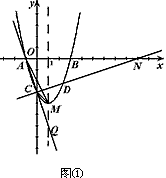 ,
,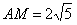
∵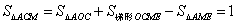
且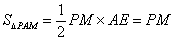 ,又
,又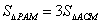 ∴
∴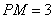
设P(1,m)
①当点P在点M上方时,PM=m+4=3,
∴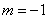 ,∴P(1,-1)
,∴P(1,-1)
②当点P在点M下方时,PM=-4-m=3, ∴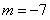
∴P(1,-7)
综上所述,点P的坐标为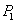 (1,-1),
(1,-1),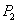 (1,-7)
(1,-7)