问题
选择题
顶点为P的圆锥的轴截面积是等腰直角三角形,A是底面圆周上的点,O为底面圆的圆心,AB⊥OB,垂足为B,OH⊥PB,垂足为H,且PA=4,C为PA的中点,则当三棱锥O-HPC的体积最大时,OB的长是( )
|
答案
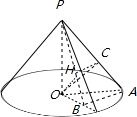
AB⊥OB,可得PB⊥AB,即AB⊥面POB,所以面PAB⊥面POB.
OH⊥PB,则OH⊥面PAB,OH⊥HC,OH⊥PC,
又,PC⊥OC,所以PC⊥面OCH.即PC是三棱锥P-OCH的高.PC=OC=2.
而△OCH的面积在OH=HC=
时取得最大值(斜边=2的直角三角形).2
当OH=
时,由PO=22
,知∠OPB=30°,OB=POtan30°=2
.2 6 3
故选D.
