假设随机变量X1,X2,X3,X4相互独立,且同分布:
PXi=0=0.6,PXi=1=0.4(i=1,2,3,4),
求行列式
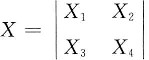 的概率分布.
的概率分布.
参考答案:记Y1=X1X4,Y2=X2X3,则X=Y1-Y2,且Y1,Y2独立同分布:
P{Y1=1}=P{X1=1,X4=1}=P{X1=1}P{X4-1}=0.16=P{Y2=1};
P{Y1=0}=1-P{Y1=1}=0.84=P{Y2=0}.
X=Y1-Y2的所有可能取值为-1、0、1,且
P{X=-1}=P{Y1-Y2=-1}=P{Y1=0,Y2=1}=P{Y1=0}P{Y2=1}
=0.84×0.16=0.1344:
P{X=1}=P{Y1-Y2=1}=P{Y1=1,Y2=0}=P{Y1=1}P{Y2=0}
=0.16×0.84=0.1344:
P{X=0}=1-2×0.1344=0.7312.
于是行列式的概率分布

[评注] 本题实际上考查的是多个随机变量函数的分布.另外{X=0}的概率也可如下计算:
P{X=0}=P{Y1-Y2=0}=P{Y1=0,Y2=0}+P{Y1=1,Y2=1}
=P{Y1=0)P{Y2=0}+P{Y1=1}P{Y2=1}
=0.84×0.84+0.16×0.16
=0.7312.
解析:[考点提示] X由二阶行列式表示,实际上是随机变量X1、X2、X3、X4的函数,仍是一个随机变量.且X=X1X4-X2X3,根据X1、X2、X3、X4独立同分布,有X1X4与X3X2独立同分布,因此可先求出X1X4与X2X3的分布律,再求X的分布律.
