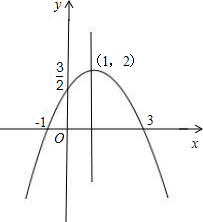问题
解答题
已知二次函数y=-
(1)求函数图象的顶点坐标和对称轴; (2)求函数图象与坐标轴的交点坐标; (3)画出此函数图象的草图,并根据图象回答:x为何值时,y>0? |
答案
(1)原式可化为y=-
(x2-2x+1-1)+1 2
=-3 2
(x-1)2+2;1 2
故顶点为(1,2),对称轴:直线x=1.
(2)当x=0时,y=
;则与y轴交点(0,3 2
);3 2
当y=0时,-
x2+x+1 2
=0,3 2
解得x1=-1,x2=3,
故与轴交点为(-1,0),(3,0).
(3)如图所示:
当-1<x<3时,y>0.