问题
填空题
若二次函数y=-x2+2(m-1)x+2m-m2的图象关于y轴对称,则m的值为:______.此函数图象的顶点和它与x轴的两个交点所确定的三角形的面积为:______.
答案
∵二次函数y=-x2+2(m-1)x+2m-m2的图象关于y轴对称,
∴2(m-1)=0,
∴m=1.
∴二次函数解析式为y=-x2+1.
当y=0时,
-x2+1=0,
解得x=±1,
图象与x轴的交点坐标为(1,0),(-1,0).
当x=0时,y=1,
则函数顶点坐标为(0,1).
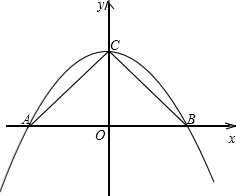
如右图:
则S△ABC=
AB•OC=1 2
×2×1=1.1 2
故答案为1,1.