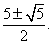问题
解答题
已知抛物线y=x2+bx+c经过点A(0,5)和B(3,2)点。
(1)求抛物线的解析式;
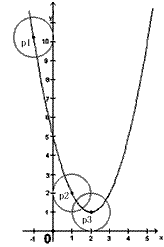
(2)现有一半径为1,圆心P在抛物线上运动的动圆,问当⊙P在运动过程中,是否存在⊙P与坐标轴相切的情况?若存在,请求出圆心P的坐标;若不存在,请说明理由;
(3)若⊙Q的半径为r,点Q在抛物线上,当⊙Q与两坐标轴都相切时,求半径r的值。
答案
解:(1)由题意,得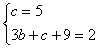 |
解得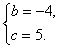 |
抛物线的解析式为 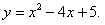 |
| (2)如图1,当⊙P在运动过程中,存在⊙P与坐标轴相切的情况。 |
设点P坐标为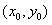 ,则当⊙P与y轴相切时, ,则当⊙P与y轴相切时, |
有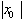 =1, =1,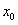 = =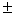 1 1 |
由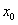 = -1,得 = -1,得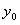 = =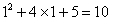 |
∴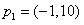 由 由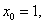 得 得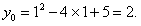 |
∴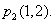 |
当⊙P与x轴相切时有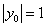 |
抛物线开口向上,且顶点在x轴的上方,∴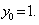 |
由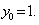 得
得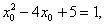
解得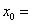 2,
2, 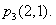
综上所述,符合要求的圆心P有三个,其坐标分别为:
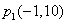 ,
,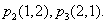
(3)设点Q坐标为 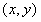 ,则当⊙Q与两条坐标轴都相切时,有
,则当⊙Q与两条坐标轴都相切时,有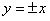
由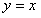 ,得
,得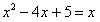
即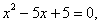 解得:
解得: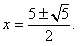
由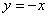 ,得
,得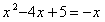
即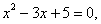 此方程无解。
此方程无解。
∴⊙Q的半径为r=