问题
解答题
（本小题满分12分）
5个人排成一排，按下列要求各有多少种不同的排法？
（1）其中甲不站排头，乙不站排尾；
（2）其中甲、乙2人必须相邻；
（3）其中甲、乙2人不能相邻；
（4）其中甲、乙中间有且只有1人；
（5）其中甲只能站在乙的左侧．
答案
（1）（捆绑法）将甲、乙二人绑在一起作为一个元素与其他3个元素作全排列，共有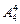
种，甲、乙内部有
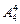
种排法，故共有=48种． 3分
（2）（插空法）先将甲、乙2人之外的3人排好，有
种排法，这三人之间及两端形成四个空位，再将甲、乙插入到这4个空中去，有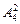
种排法，故共有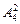=72种．
3分
（3）甲、乙二人有种排法，再从剩下的3人中选1人插入他们之间，有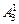
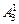
种方法，然后将这三人看作一个元素，和其他2个元素做全排列，有种，故共有=36种．
（4）五个人的全排列为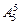
种，这些排列中甲、乙的不同顺序的排法有，但只有一种是符合要求的，故满足条件的排法有
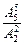=60种