问题
填空题
若线性方程组
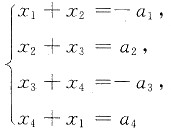
有解，则常数a1，a2，a3，a4应满足条件______．
答案
参考答案：a1+a2+a3+a4=0
解析：[考点提示] 方程组有解[*]，对增广矩阵[*]作初等行变换即得．
[解题分析]
[详解1] 对增广矩阵作初等行变换化为阶梯形．
[*]
可知r(A)=3，又由于原方程有解，则[*]，所以a1+a2+a3+a4=0．
[详解2] 若线性方程组有解，则其系数矩阵A与增广矩阵[*]有相同的秩．
[*]
因[*]，知A的秩小于4，所以[*]的秩也应小于4，从而知[*]即a1+a2+a3+a4=0．
[评注] 本题主要考查非齐次方程组有解的条件，常规方法是将增广矩阵[*]施行初等列变换(因为只需判定解的情况，即只需知道A和[*]的秩为阶梯形矩阵，得r(A)和[*]，即知有解的条件．