已知二次函数y=x2-mx+m-2。
（1）求证：无论m为任何实数，该二次函数的图象与x轴都有两个交点；
（2）当该二次函数的图象经过点（3，6）时，求二次函数的解析式；
（3）将直线y=x向下平移2个单位长度后与（2）中的抛物线交于A、B两点（点A在点B的左边），一个动点P自点A出发，先到达抛物线的对称轴上的某点E，再到达x轴上的某点F，最后到达点B，求使点P运动的总 路径最短的点E、点F的坐标，并求出这个最短总路径的长。
解：（1）令y=0，则x2-mx+m-2=0，
∵△=（-m）2-4（m-2）=m2-4m+8=（m-2）2+4，
又∵（m-2）2≥0，
∴（m-2）2+4>0，
即△>0，
∴无论m为任何实数，一元二次方程x2-mx+m-2=0总有两不等实根，
∴该二次函数图象与x轴都有两个交点；
（2）∵二次函数y=x2-mx+m-2的图象经过点（3，6），
∴32-3m+m-2=6，
解得m=
，
∴二次函数的解析式为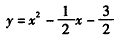
；
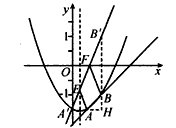
（3）如图，将y=x的图象向下平移2个单位长度后，
其解析式为：y=x-2，
解方程组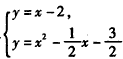
得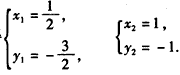
∴直线y=x-2与抛物线y=x2-
x-
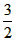的交点为A（
，
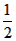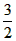），B（1，-1），
∴点A关于对称轴x=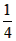
的对称点是A′（0，-
），
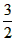点B关于x轴的对称点是B′（1，1），
设过点A′B′的直线解析式为y=kx+b，
∴
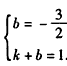解得
∴直线A′B′的解析式为y=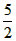
x-
∴直线A′B′与x轴的交点为F（
，0），
与直线x=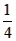
的交点为E（，-
），
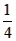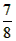则点E（
，-
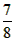）、F（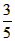
，0）为所求，
过点B′作B′H ⊥AA′于点H，
∴B′H=
，HA′=1，
在Rt△A′B′H中，
∴所求最短总路径的长为AE+EF+FB=A′B′=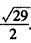
。
| Martin Luther King, Jr., is well known for his work in civil rights and for his many famous speeches, among them his moving "I Have A Dream" speech. But fewer people know much about King’s childhood. M. L., as he was called, was born in 1929 in Atlanta, Georgia, at the home of his maternal grandfather. M.L.’s grandfather, the Reverend A. D. Williams, purchased their home on Auburn Avenue in 1909, 20 years before M. L. was born. The Reverend Williams, an eloquent speaker, played an important role in the community since so many people’s lives centered around the church. He allowed his church and his home to be used as a meeting place for a number of organizations dedicated to the education and social advancement of blacks. M.L. grew up in this atmosphere, with his home being used as a community gathering place, and was no doubt influenced by it. M. L.’s childhood was not especially eventful. His father was a minister and his mother was a musician. He was the second of three children, and he attended all-black schools in a black neighborhood. The neighborhood was not poor, however. Auburn Avenue was the main artery through a prosperous neighborhood that had come to symbolize achievement for Atlanta’s black people. It was an area of banks, insurance companies, builders, jewelers, tailors, doctors, lawyers and other black-owned or black-operated businesses and services. Even in the face of Atlanta’s segregation, the district thrived. Dr. King never forgot the community spirit he had known as a child, nor did he forget the racial prejudice that was a seemingly insurmountable barrier that kept black Atlantans from mingling with whites. |
The word "it" underlined in Paragraph 2 refers to ______.
A．achievement
B．neighborhood
C．segregation
D．services