问题
解答题
已知函数f(x)=
（1）求f（x）的单调区间； （2）若f（x）在[0，+∞）上的最小值是0，求实数a的取值范围． |
答案
（1）f′（x）=
（x＞-1）．x(ax+a-1) x+1
①当a=0时，f′(x)=
，∴函数f（x）的单调递增区间是（-1，0），单调递减区间是（0，+∞）；-x x+1
②当a＞0时，f′（x）=
，ax(x-
)1-a a x+1
令f′（x）=0，解得x1=0，x2=
．1-a a
当0＜a＜1时，x1＜x2，函数f（x）的单调递增区间是（-1，0）和(
，+∞)，单调递减区间是(0，1-a a
)；1-a a
当a=1时，f′(x)=
在（-1，+∞）上单调递增；x2 x+1
当a＞1时，-1＜
＜0，∴函数f（x）的单调递增区间是(-1，1-a a
)和（0，+∞），单调递减区间是(1-a a
，0)．1-a a
（2）由（1）可知：①a=0时不符合题意；
②当0＜a＜1时，函数f（x）在(0，
)上单调递减，在(1-a a
，+∞)单调递增，1-a a
由题意可知f（x）min=f(
)＜f（0）=0，不符合题意，应舍去；1-a a
③当a≥1时，函数f（x）在[0，+∞）上单调递增，
故f（x）min=f（0）=0满足题意．
综上可知：a的取值范围是[1，+∞）．
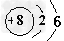，从图中你获得的信息有（写二条即可）______________________。实验室制取氧气的化学方程式是____________。能产生温室效应的气体有（至少写三种）_______________。