问题
解答题
已知二次函数y=ax2+4ax+4a-1的图象是C1。
（1）求C1关于点R（1，0）中心对称的图象C2的函数解析式；
（2）在（1）的条件下，设抛物线C1、C2与y轴的交点分别为A、B，当AB=18 时，求a的值。
答案
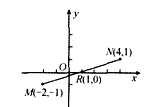
解：（1）由y=a（x+2）2-1，可知抛物线C1的顶点为M（-2，-1），由图知点M（-2，-1）关于点R（1，0）中心对称的点为N（4，1），以N（4，1）为顶点，与抛物线C1关于点R（1，0）中心对称的图象C2也是抛物线，且C1与C2的开口方向相反，故抛物线C2的函数解析式为y=-a（x-4）2+1，
即y=-ax2+8ax-16a+1；
（2）令x=0，得抛物线C1、C2与y轴的交点A、B的纵坐标分别为4a-1和-16a+1，
∴
∴
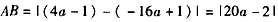
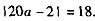
当a≥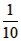
时，有20a-2=18，得a=1；
当a＜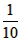
时有2-20a=18，得a=-
。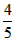