问题
选择题
若n的展开式中前三项的系数成等差数,则展开式中x4项的系数为( )
A.6
B.7
C.8
D.9
答案
答案:B
分析:求出)n的展开式中前三项的系数Cn0、 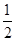
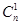 、
、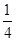
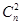 , 由等差数列知识求出n,再利用通项公式求出x4项的系数即可.
, 由等差数列知识求出n,再利用通项公式求出x4项的系数即可.
解:因为n的展开式中前三项的系数Cn0、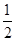
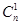 、
、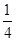
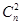 成等差数列,
成等差数列,
所以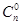 +
+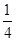
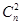 =
=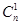 ,即n2-9n+8=0,解得:n=8或n=1(舍).
,即n2-9n+8=0,解得:n=8或n=1(舍).
Tr+1=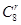 x8-r(
x8-r(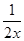 )r=(
)r=(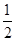 )r
)r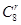 x8-2r.
x8-2r.
令8-2r=4可得,r=2,所以x4的系数为(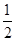 )2
)2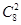 =7,
=7,
故选B

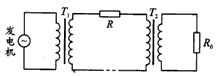
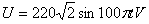 ,降压变压器的副线圈与阻值R0=11 Ω的电阻组成闭合电路,若将变压器视为理想变压器,则下列说法中正确的是
,降压变压器的副线圈与阻值R0=11 Ω的电阻组成闭合电路,若将变压器视为理想变压器,则下列说法中正确的是