问题
解答题
函数y=ax2(a≠0)与直线y=2x-3交于点(1,b)。
(1)求a和b的值;
(2)求抛物线y=ax2的解析式,并求顶点坐标及对称轴;
(3)x取何值时,二次函数y=ax2中的y随x的增大而增大?
(4)求抛物线和直线y=-2的两个交点与抛物线顶点所构成的三角形的面积。
答案
解:(1)把x=1,y=b代入y=2x-3,解得b=-1,
∴交点坐标是(1,-1),
再把x=1,y=-1代入y=ax2,
解得a=-1,
∴a=-1,b=-1;
(2)抛物线的解析式为y=-x2,顶点坐标为(0,0),对称轴为y轴;
(3)当x<0时,y随x的增大而增大;
(4)设直线y=-2与抛物线y=-x2交于A、B两点,如图,
则 ,
,
∴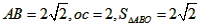 。
。