问题
解答题
（1）由数字0，1，2，3，4，5组成没有重复数字的六位数，其中个位数字小于十位数字的共有多少个？
（2）某高校从某系的10名优秀毕业生中选4人分别到西部四城市参加中国西部经济开发建设，其中甲同学不到银川，乙不到西宁，共有多少种不同派遣方案？
（3）将4个相同的白球、5个相同的黑球、6个相同的红球放入4各不同的盒子中的3个中，使得有一个空盒且其他盒子中球的颜色齐全的不同放法有多少种？
答案
解：（1）按题意，个位数字只可能是0，1，2，3，4共5种情况，分别有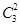
个，
个，合并总计300个,
（2）因为甲乙有限制条件，所以按照是否含有甲乙来分类，有以下四种情况：
①若甲乙都不参加，则有派遣方案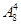
种；②若甲参加而乙不参加，先安排甲有3种方法，然后安排其余学生有
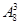方法，所以共有
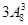；③若乙参加而甲不参加同理也有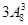种；④若甲乙都参加，则先安排甲乙，有7种方法，然后再安排其余8人到另两个城市有
种，共有
方法.所以共有不同的派遣方法总数为
种
（3）先从4个盒子中选三个放置小球有
种方法。注意到小球都是相同的，我们可以采用隔板法。为了保证三个盒子中球的颜色齐全，可以在4个相同的白球、5个相同的黑球、6个相同的红球所产生的3个、4个5个空挡中分别插入两个板。各有、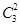
、
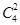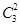
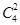
种方法。由分步计数原理可得=720种