问题
填空题
如图,在四面体ABCD中,P、Q分别为棱BC与CD上的点,且BP=2PC,CQ=2QD.R为棱AD的中点,则点A、B到平面PQR的距离的比值为 .
答案
.

:A、B到平面PQR的距离分别为三棱锥APQR与BPQR的以三角形PQR为底的高.故其比值等于这两个三棱锥的体积比.
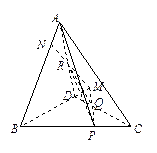
VAPQR=VAPQD=×VAPCD=××VABCD=VABCD;
又,SBPQ=SBCD-SBDQ-SCPQ=(1--×)SBCD=SBCD,
VRBPQ=VRBCD=×VABCD=VABCD.∴ A、B到平面PQR的距离的比=1∶4.
又,可以求出平面PQR与AB的交点来求此比值:
在面BCD内,延长PQ、BD交于点M,则M为面PQR与棱BD的交点.
由Menelaus定理知,··=1,而=,=,故=4.
在面ABD内,作射线MR交AB于点N,则N为面PQR与AB的交点.
由Menelaus定理知,··=1,而=4,=1,故=.
∴ A、B到平面PQR的距离的比=1∶4.
