已知:关于x的一元二次方程-x2+(m+4)x-4m=0,其中0<m<4。
(1)求此方程的两个实数根(用含m的代数式表示)
(2)设抛物线y=-x2+(m+4)x-4m与x轴交于A、B两点(A在B的左侧),与y轴交于点C,若点D的坐标为(0,-2),且AD·BD=10,求抛物线的解析式;
(3)已知点E(a,y1)、F(2a,y2)、G(3a,y3)都在(2)中的抛物线上,是否存在含有y1、y2、y3,且与n无关的等式?如果存在,试写出一个,并加以证明;如果不存在,说明理由。
解:(1)将原方程整理,得x2-(m+4)x+4m=0,
∵(0<m<4),△=b2-4ac=[-(m+4)]2-4(4m)=m2-8m+16=(m-4)2>0
∴x=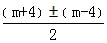
∴x=m或x=4;
(2)由(1)知,抛物线y=-x2+(m+4)x-4m与x轴的交点分别为(m,0)、(4,0),
∵A在B的左侧,0<m<4,
∴A(m,0),B(4,0),则AD2=OA2+OD2=m2+22=m2+4
BD2=OB2+OD2=42+22=20
∵AD·BD=10
∴AD2·BD2=100
∴20(m2+4)=100,解得m=±1
∵0<m<4,
∴m=1,
∴m+4=5,-4m=-4,
∴抛物线的解析式为y=x2+5x-4;
(3)存在含有y1、y2、y3,且与a无关的等式,如:y3=3(y1-y2)-4(答案不唯一);
证明:由题意可得y1=-a2+5a-4,y2=-4a2+10a-4,y3=-9a2+15a-4,
∵左边=y3=-9a2+15a-4,
右边=-3(y1-y2)-4=-3[(-a2+5a-4)-(-4a2+10a-4)]-4=-9a2+15a-4,
∴左边=右边,∴y3=-3(y1-y2)-4成立。
