问题
解答题
为把产品打入国际市场，某企业决定从下面两个投资方案中选择一个进行投资生产。
方案一：生产甲产品，每件产品成本为a万美元（a为常数，且3＜a＜8），每件产品销售价为10万美元，每年最多可生产200件；
方案二：生产乙产品，每件产品成本为8万美元，每件产品销售价为18万美元，每年最多可生产120件，另外，年销售x件乙产品时需上交0.05x2万美元的特别关税，在不考虑其它因素的情况下：
（1）分别写出该企业两个投资方案的年利润y1、y2与相应生产件数x（x为正整数）之间的函数关系式，并指出自变量的取值范围；
（2）分别求出这两个投资方案的最大年利润；
（3）如果你是企业决策者，为了获得最大收益，你会选择哪个投资方案？
答案
解：（1）
（1≤x≤200，x为正整数）
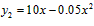（1≤x≤120，x为正整数）
（2）①∵3＜a＜8，
∴10-a＞0，y1是x的正比例函数即y1随x的增大而增大
∴当x=200时，y1最大值=（10-a）×200=2000-200a（万美元）
②
∵-0.05＜0，
∴x=100时，y2最大值=500（万美元）；
（3）由2000-200a＞500，得a＜7.5，
∴当3＜a＜7.5时，选择方案一；
由2000-200a=500，得a=7.5，
∴当a=7.5时，选择方案一或方案二均可；
由2000-200a<500，得a>7.5，
∴当7.5＜a＜8时，选择方案二。
