问题
解答题
已知f(x)=
(1)求f(x)的单调区间; (2)若y=f(x)的图象与x轴有三个交点,求实数a的取值范围. |
答案
(1)f′(x)=x2-(a+1)x+a=(x-1)(x-a),
当a>1时,由f′(x)>0得x<1或x>a,
∴x∈(-∞,1)和(a,+∞)时,f(x)单调递增,x∈(1,a)时,f(x)单调递减;
当a<1时,由f′(x)>0,得x<a或x>1,
∴x∈(-∞,a)和(1,+∞)时,f(x)单调递增,x∈(a,1)时,f(x)单调递减.
(2)由(1)知x=1和x=a是f(x)得极值点,
a>1时,f(1)是极大值,f(a)是极小值;a<1时,f(a)是极大值,f(1)是极小值,
又y=f(x)的图象与x轴有三个交点,
∴f(1)•f(a)<0,即
(a-1 2
)•[-1 3
a2(a-3)]<0,1 6
∴(a-3)(a-
)>0,1 3
∴a>3或a<
.1 3

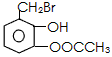 与足量NaOH溶液反应的化学方程式______________________________
与足量NaOH溶液反应的化学方程式______________________________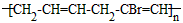 的单体的结构简式_____________________
的单体的结构简式_____________________