问题
解答题
在直角坐标系xOy中，O为坐标原点，A，B，C三点的坐标分别为A（5，0），B（0，4），C（-1，0），点M和点N在x 轴上（点M在点N的左边），点N在原点的右边，作MP⊥BN，垂足为P（点P在线段BN上，且点P与点B不重合），直线MP与y，轴交于点C，MG=BN。
（1）求经过A，B，C三点的抛物线的解析式；
（2）求点M的坐标；
（3）设ON=t，△MOG的面积为s，求s与t的函数关系式，并写出自变量t的取值范围；
（4）过点B作直线BK平行于x轴，在直线BK上是否存在点R，使△ORA为等腰三角形，若存在，请直接写出点R的坐标；若不存在，请说明理由。
答案
解：（1）设所求抛物线的解析式为y=ax2+bx+c（a≠0），
由题意，得：
解得：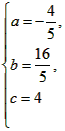
∴所求的解析式为y=-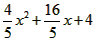
；
（2）依题意，分两种情况：
①当点M在原点的左边（如图甲）时，
在Rt△BON中，∠1+∠3=90°，
∵MP⊥BN，
∴∠2+ ∠3=90°，
∴∠1=∠2，
在Rt△BON和Rt△MOG中，
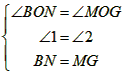
∴Rt△BON≌Rt△MOG，
∴OM=OB=4，
∴M点坐标为（-4，0），
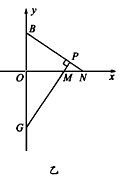
②当点M在原点的右边（如图乙）时，
同理可证：OM=OB=4，此时M点坐标为（4，0），
∴M点坐标为（4，0）或（-4，0）；
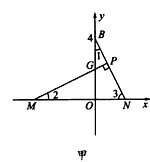
（3）图甲中，Rt△BON≌Rt△MOG，
∴OG=ON=t，
∴S=
OM·OG=
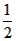·4·t=2t（其中0<t<
图乙中，同理可得S=2t，其中t>4，
∴所求的函数关系式为S=2t，
t的取值范围为t>0且t≠4；
（4）存在点R，使△ORA为等腰三角形，
其坐标为：R1（-3，4），R2（3，4），R3（2，4），R4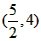
，R5（8，4）。