问题
解答题
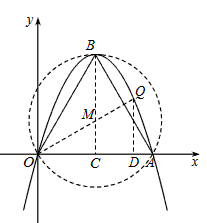
在平面直角坐标系xOy中，O是坐标原点，等边三角形OAB的一个顶点为A（2，0），另一个顶点B在第一象限内。
（1）求经过O、A、B三点的抛物线的解析式；
（2）如果一个四边形是以它的一条对角线为对称轴的轴对称图形，那么我们称这样的四边形为“筝形”。点Q在（1）的抛物线上，且以O、A、B、Q为顶点的四边形是“筝形，求点Q的坐标；
（3）设△OAB的外接圆⊙M，试判断（2）中的点Q与⊙M的位置关系，并通过计算说明理由。
答案
解：（1）过B作BC⊥x轴于C，
∵等边三角形OAB的一个顶点为A（2，0），
∴OB=OA=2，AC=OC=1，∠BOC=60°，
∴BC=
，
∴B
，
设经过O、A、B三点的抛物线的解析式为：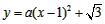
将A（2，0）代入得：
，
解得
，
∴经过O、A、B三点的抛物线的解析式为
即
；
（2）依题意分为三种情况：
（ⅰ）当以OA、OB为边时，
∵OA=OB，
∴过O作OQ⊥AB交抛物线于Q，
则四边形OAQB是筝形，且∠QOA=30°，
作QD⊥x轴于D，QD=OD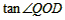
，
设Q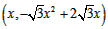
，则
，
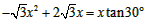解得：
，
∴Q
；
（ⅱ）当以OA、AB为边时，由对称性可知Q
；
（ⅲ）当以OB、AB为边时，抛物线上不存在这样的点Q使BOQA为筝形，
∴Q
或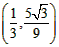
；
（3）点Q在⊙M内，
由等边三角形性质可知
的外接圆圆心M是（2）中BC与OQ的交点，
当Q
时，
∵MC∥QD，
∴△OMC∽△OQD，
∴
，
∴
，
∴
，
∴
，
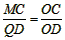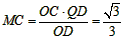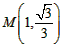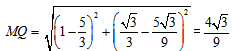又
，
∵
，
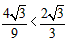∴Q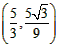
在
内，
当Q
时，由对称性可知点Q在
内，
综述，点Q在内。
