（1）300个（2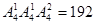）个 （3）1631个

有关数字的排列问题，一般从可从元素与位置两个角度考虑。（1）从位置上考虑，0不能在首位，共有5种排法，后三位共有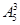种排法，不同的四位数共有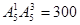个；从元素考虑，包括0共有6个数，要得到四位数有两种情况：含有0，则0不在首位，共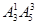种，不含0，共有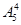个，不同的四位数共有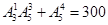个。也可用排除法解；（2）要得到奇数，首先满足个位是奇数，再满足首位不为0，最后是中间的两个数，共有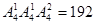个；（3）6个数字组成的自然数共有一位，两位，三位，四位，五位，六位六种情况，分类求解可得

（1）解法一：从“位置”考虑，由于0不能放在首位，因此首位数字只能有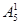种取法，其余3个数位可以从余下的5个数字（包括0）中任取3个排列，所以可以组成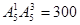个四位数；……４分  

解法二：从“元素”考虑，组成的四位数可以按有无数字0分成两类，有数字0的有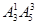个，无数字0的有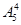个，所以共组成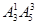+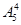=300个四位数；

解法三：“排除法”从6个元素中取4个元素的所有排列中，减去0在首位上的排列数即为所求，所以共有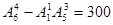个四位数；

（2）从“位置”考虑，个位数字必须是奇数有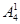种排法，由于0不能放在首位，因此首位数字只能有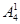种取法，其余两个数位的排法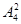有，所以共有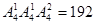个四位奇数；……８分  

（3）一位数：有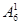=6个；两位数：有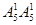=25个；

三位数：有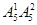=100个；四位数：有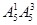=300个；

五位数：有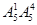=600个；六位数：有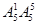=600个；

所以共有6+25+100+300+600+600=1631个自然数．　　　……1２分  

点评：解有条件限制的排列问题思路：①正确选择原理；②处理好特殊元素和特殊位置，先让特殊元素占位，或特殊位置选元素；③再考虑其余元素或其余位置；④数字的排列问题，0不能排在首位．