问题
问答题
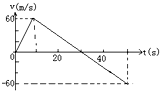
一空间探测器的质量恒为3000kg,发动机推力为恒力.探测器从无大气层的某星球表面竖直升空,升空后发动机因故障而突然关闭;如图所示为探测器从升空到回落的速度-时间图象.求:
(1)探测器发动机的推力.
(2)若该星球与地球的半径之比为1:3,它们的质量比为多少?(地球表面处g=10m/s2)
答案
(1)由速度-时间图象知,0-10s在发动机的推力作用下探测器作匀加速直线运动,10s后探测器只受重力而作匀减速直线运动.设该星球表面附近的重力加速度为g星,探测器发动机的推力为F.
在10s后:a2=
=vt-v0 t
=-3m/s20-60 20
则g星=3m/s2
在0-10s内:a1=
=6m/s260-0 10
据牛顿第二定律有F-mg星=ma1
得F=3000×3+3000×6=2.7×104N
(2)在天体表面附近的物体,有
=mgGMm R2
解得M=gR2 G
故:
=M星 M地
=g星 R 2星 g R 2地
×(3 10
)2=1 3 1 30
答:(1)探测器发动机的推力为2.7×104N.
(2)若该星球与地球的半径之比为1:3,它们的质量比为1:30.
