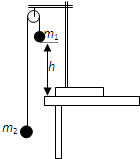
问题
解答题
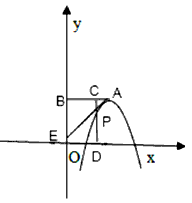
已知抛物线y=-x2+2mx-m2+2的顶点A在第一象限,过点A作AB⊥y轴于点B,C是线段AB上一点(不与点A、B重合),过点C作CD⊥x轴于点D并交抛物线于点P。
(1)若点C(1,a)是线段AB的中点,求点P的坐标;
(2)若直线AP交y轴的正半轴于点E,且AC=CP,求△OEP的面积S的取值范围。
答案
解:(1)依题意得顶点A的坐标为(2,a),
设P(1,n)据x=-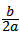 ,得A点的横坐标为m,即m=2,
,得A点的横坐标为m,即m=2,
所以y=x2+4x-2,把P点的坐标代入得n=1,
即P点的坐标为(1,1);
(2)把抛物线化为顶点式:y=-(x-m)2+2,
可知A(m,2),
设C(n,2),
把n代入y=-(x-m)2+2得y=-(n-m)2+2,
所以P(n,-(n-m)2+2)
∵AC=CP
∴m-n=2+(m-n)2-2,
即m-n=(m-n)2,
∴m-n=0或m-n=1,
又∵C点不与端点A、B重合
∴m≠n,
即m-n=1,
则A(m,2),P(m-1,1)
由AC=CP可得BE=AB
∵OB=2
∴OE=2-m,
∴△OPE的面积S=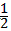 (2-m)(m-1)=-(m-
(2-m)(m-1)=-(m-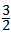 )2+
)2+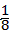 (1<m<2),
(1<m<2),
∴0<S<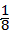 。
。
问答题