问题
解答题
在平面直角坐标系中,已知抛物线y=-x2+bx+c与x轴交于点A、B(点A在点B的左侧),与y轴的正半轴交于点C,顶点为E。
(Ⅰ)若b=2,c=3,求此时抛物线顶点E的坐标;
(Ⅱ)将(Ⅰ)中的抛物线向下平移,若平移后,在四边形ABEC中满足S△BCE=S△ABC,求此时直线BC的解析式;
(Ⅲ)将(Ⅰ)中的抛物线作适当的平移,若平移后,在四边形ABEC中满足S△BCE=2S△AOC,且顶点E恰好落在直线y=-4x+3上,求此时抛物线的解析式。
答案
解:(Ⅰ)当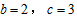 时,抛物线的解析式为
时,抛物线的解析式为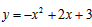 ,
,
即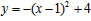 ,
,
∴ 抛物线顶点的坐标为(1,4);
(Ⅱ)将(Ⅰ)中的抛物线向下平移,则顶点E在对称轴x=1上,有b=2,
∴抛物线的解析式为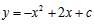 (c>0),
(c>0),
∴此时,抛物线与y轴的交点为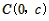 ,顶点为
,顶点为 ,
,
∵方程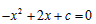 的两个根为
的两个根为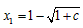 ,
,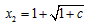 ,
,
∴此时,抛物线与x轴的交点为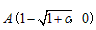 ,
,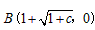
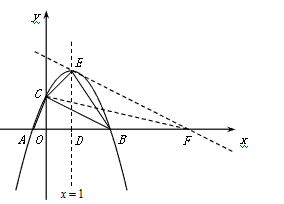
如图,过点作EF∥CB与x轴交于点F,连接CF,则S△BCE=S△BCF,
∵S△BCE = S△ABC,
∴S△BCF=S△ABC,
∴ ,
,
设对称轴x=1与x轴交于点D,则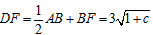 ,
,
由EF∥CB,得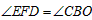 ,
,
∴Rt△EDF∽Rt△COB,
有 ,
,
∴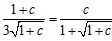 ,
,
结合题意,解得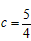 ,
,
∴点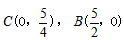 ,
,
设直线BC的解析式为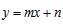 ,则
,则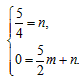
解得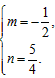
∴直线的解析式为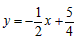 ;
;
(Ⅲ)根据题意,设抛物线的顶点为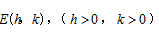 ,
,
则抛物线的解析式为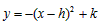 ,
,
此时,抛物线与y轴的交点为 ,与x轴的交点为
,与x轴的交点为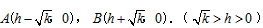 ,
,
过点E作EF∥CB与x轴交于点F,连接CF,
则S△BCE=S△BCF,
由S△BCE=2S△AOC,
∴S△BCF=2S△AOC,
得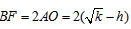 ,
,
设该抛物线的对称轴与x轴交于点D,
则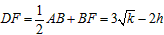 ,
,
于是,由Rt△EDF∽Rt△COB,有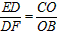 ,
,
∴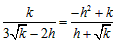 ,
,
即 ,
,
结合题意,解得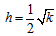 ,①
,①
∵点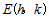 在直线
在直线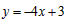 上,有
上,有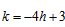 ,②
,②
∴由①②,结合题意,解得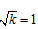 ,
,
有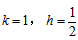 ,
,
∴抛物线的解析式为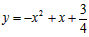 。
。
