已知关于x的方程mx2-(3m-1)x+2m-2=0。
(1)求证:无论m取任何实数时,方程恒有实数根;
(2)若关于x的二次函数y= mx2-(3m-1)x+2m-2的图象与x轴两交点间的距离为2时,求抛物线的解析式;
(3)在直角坐标系xoy中,画出(2)中的函数图象,结合图象回答问题:当直线y=x+b与(2)中的函数图象只有两个交点时,求b的取值范围。
解:(1)分两种情况讨论:
①当m=0 时,方程为x-2=0,
∴x=2 方程有实数根;
②当m≠0时,则一元二次方程的根的判别式
△=[-(3m-1)]2-4m(2m-2)=m2+2m+1=(m+1)2≥0
不论m为何实数,△≥0成立,
∴方程恒有实数根综合①②,可知m取任何实数,方程mx2-(3m-1)x+2m-2=0恒有实数根;
(2)设x1,x2为抛物线y= mx2-(3m-1)x+2m-2与x轴交点的横坐标,
则有x1+x2=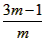 ,x1·x2=
,x1·x2=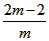
由| x1-x2|=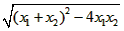 =
=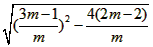 =
=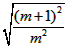 =
=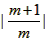 ,
,
由| x1-x2|=2得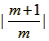 =2,
=2,
∴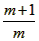 =2或
=2或 =-2
=-2
∴m=1或m=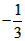
∴所求抛物线的解析式为:y1=x2-2x或y2=-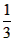 x2+2x-
x2+2x-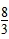
即y1= x(x-2)或y2=-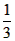 (x-2)(x-4)
(x-2)(x-4)
其图象如右图所示;
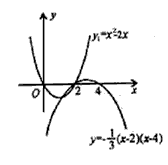
(3)在(2)的条件下,直线y=x+b与抛物线y1,y2组成的图象只有两个交点,结合图象,求b的取值范围,
当y1=y时,得x2-3x-b=0,△=9+4b=0,解得b=-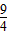 ;
;
同理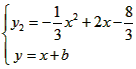 ,可得△=9-4(8+3b)=0,得b=-
,可得△=9-4(8+3b)=0,得b=-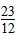 ,
,
观察函数图象可知当b<-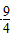 或b>-
或b>-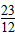 时,直线y=x+b与(2)中的图象只有两个交点,
时,直线y=x+b与(2)中的图象只有两个交点,
由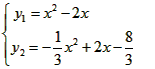
当y1=y2时,有x=2或x=1
当x=1时,y=-1,
所以过两抛物线交点(1,-1),(2,0)的直线y=x-2,
综上所述可知:当b<-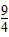 或b>-
或b>-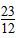 或b=-2时,直线y=x+b与(2)中的图象只有两个交点。
或b=-2时,直线y=x+b与(2)中的图象只有两个交点。
