解：(Ⅰ)组成无重复数字的自然数共有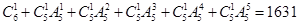个；

(Ⅱ)重复数字的四位偶数共有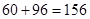个；

(Ⅲ)比4023大的数共有60＋48＋6＋1＝115个.

本试题主要是考查了排列与组合的运用。利用排列数公式和组合数公式来计算求解，注意对于特殊元素优先考虑。

(1)首先考虑0的特殊安排，然后其余的任意排列即可

(2)由于是偶数，末尾数必须是偶数0,2,4，分情况讨论得到结论

（3）要找到比比4023大的数共有多少个，首先对于首位是5,4，的情况分别讨论可得。

解：(Ⅰ)组成无重复数字的自然数共有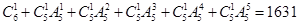个……………………………4分

(Ⅱ)无重复数字的四位偶数中个位数是0共有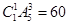个；……………………6分

个位数是2或4共有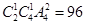个

所以，重复数字的四位偶数共有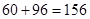个    ……………………………9分

(Ⅲ)无重复数字的四位数中千位数字是5的共有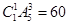个，

千位数字是4、百位数字是1、2、3、5之一的共有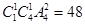个，

千位数字是4、百位数字是0、十位数字是3、5之一的共有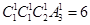个，

千位数字是4、百位数字是0、十位数字是2、个位数字只能是5有1个.

所以，比4023大的数共有60＋48＋6＋1＝115个.        ……………14分