问题
解答题
已知:二次函数y=ax2+bx-2的图象经过点(1,0),一次函数图象经过原点和点(1,-b),其中a>b且a、b为实数。
(1)求一次函数的表达式(用含b的式子表示);
(2)试说明:这两个函数的图象交于不同的两点;
(3)设(2)中的两个交点的横坐标分别为x1、x2,求|x1-x2|的范围。
答案
解:(1)∵一次函数过原点,
∴设一次函数的解析式为y=kx,
∵一次函数过(1,-b),
∴y=-bx,
(2)∵y=ax2+bx-2,
过(1,0)即a+b=2,
由 得,
得,
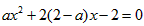 ①
①
∵△=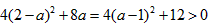 ,
,
∴方程①有两个不相等的实数根,
∴方程组有两组不同的解,
∴两函数有两个不同的交点;
(3)∵两交点的横坐标x1、x2分别是方程①的解,
∴ ,
,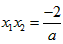
∴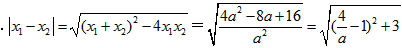
或由求根公式得出,
∵a>b>0,a+b=2,
∴2>a>1,
令函数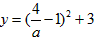 ,
,
∵在1<a<2时y随a增大而减小,
∴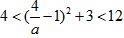
∴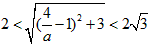 ,
,
∴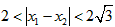 。
。
