如图1所示,abcd是位于竖直平面内的正方形闭合金属线框,其质量为m,电阻为R.在金属线框的下方有一匀强磁场区域,PQ和P´Q´是该匀强磁场区域的水平边界,并与线框的bc边平行,磁场方向与线框平面垂直.现金属线框由距PQ某一高度处从静止开始下落,经时间t0后刚好到达PQ边缘,速度为v0,假设线框所受的空气阻力恒定.图2是金属线框由静止开始下落到完全穿过匀强磁场区域过程中的速度-时间图象.
试求:(1)金属线框的边长;
(2)金属线框由静止开始下落到完全穿过匀强磁场区域的总位移;
(3)金属线框在进入匀强磁场区域过程中流过其横截面的电荷量;
(4)金属线框在整个下落过程中所产生的焦耳热.
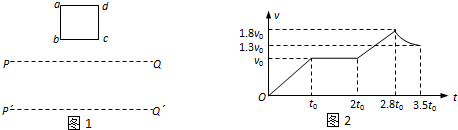
(1)由图象知,金属框进入磁场过程中做匀速直线运动,运动时间为t0,则线框的边长为 l=v0t0.
(2)由v-t图象得:线框进入磁场前:s1=0.5v0t0
线框进入磁场过程:s2=v0t0
线框在磁场内匀加速运动:s3=
×(v0+1.8v0)×0.8t0=1.12v0t01 2
线框穿出磁场和进入磁场位移相等:s4=s2=v0t0
所以:总位移为 s总=s1+s2+s3+s4=3.62v0t0
(3)线框刚进入磁场时作匀速运动,则有:F安+f=mg
即
+f=mg;B2l2v0 R
l=v0t0
线框进入磁场前作匀加速运动:mg-f=ma=mv0 t0
联立解得:B=mRt0 v0t02
在进入匀强磁场区域过程中流过线框横截面的电荷量:q=It=
t0=Bl v0 R v0 mRt0 R
(4)全过程用动能定理,得:(mg-f)s总-Q=
m(1.3v0)2-01 2
解得 Q=2.775mv02
答:
(1)金属线框的边长是v0t0.;
(2)金属线框由静止开始下落到完全穿过匀强磁场区域的总位移是3.62v0t0;
(3)金属线框在进入匀强磁场区域过程中流过其横截面的电荷量是
;v0 mRt0 R
(4)金属线框在整个下落过程中所产生的焦耳热是2.775m
.v 20
