问题
解答题
已知抛物线y=ax2+bx+c交x轴于A、B两点，交y轴于点C（0，8），若抛物线的对称轴为直线x=-1，且△ABC的面积为40。
（1）求这条抛物线的函数关系式；
（2）在直线BC上，是否存在这样的点Q，使得点Q到直线AC的距离为5？若存在，请求出符合条件的点Q的坐标；若不存在，请说明理由。
答案
解：（1）∵S△ABC=
AB·OC=
AB×8=40，
∴AB=10，
∵对称轴为直线x=-1，
∴A（-6，0），B（4，0），
∴设y=a（x+6）（x-4），
由抛物线过点C（0，8）得a=-
，
∴y=-
x2-x+8；
（2）存在这样的点Q，可求得直线BC：y=-2x+8，
利用面积法或相似的方法可求得符合条件的点Q有两个，分别为Q1 （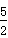
，3），Q2 （-
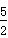，13）。