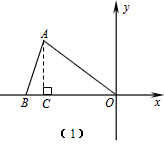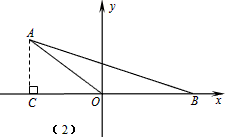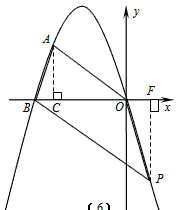已知直角坐标系中有一点A（-4，3），点B在x轴上，△AOB是等腰三角形。
（1）求满足条件的所有点B的坐标；
（2）求过O，A，B三点且开口向下的抛物线的函数表达式（只需求出满足条件的一条即可）；
（3）在（2）中求出的抛物线上存在点P，使得以O，A，B，P四点为顶点的四边形是梯形，求满足条件的所有点P的坐标及相应梯形的面积。
解：作AC⊥x轴，由已知得OC=4，AC=3，OA=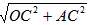
=5，
（1）当OA=OB=5时，
如果点B在x轴的负半轴上，如图（1），点B的坐标为（-5，0），
如果点B在x轴的正半轴上，如图（2），点B的坐标为（5，0），
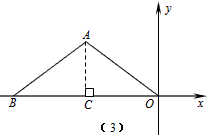
当OA=AB时，点B在x轴的负半轴上，如图（3），
BC=OC，则OB=8，点B的坐标为（-8，0），
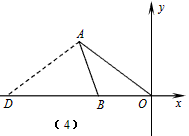
当AB=OB时，点B在x轴的负半轴上，如图（4），
在x轴上取点D，使AD=OA，可知OD=8，
由∠AOB=∠OAB=∠ODA，可知△AOB∽△ODA，则
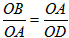，解得OB=
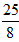，点B的坐标为（-
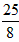，0）；
（2）当AB=OA时，抛物线过O（0，0），A（-4，3），B（-8，0）三点，
设抛物线的函数表达式为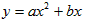
，可得方程组
，
解得a=
，b=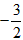
，
，
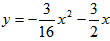（当OA=OB时，同理得
）
（3）当OA=AB时，若BP∥OA，如图（5），作PE⊥x轴，
则∠AOC=∠PBE，∠ACO=∠PEB=90°，△AOC∽△PBE，
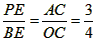，设BE=4m，PE=3m，则点P的坐标为（4m-8，-3m），
代入
，解得m=3，
则点P的坐标为（4，-9），
S梯形ABPO=S△ABO+S△BPO=48，
若OP∥AB（图略），根据抛物线的对称性可得点P的坐标为（-12，-9），
S梯形AOPB=S△ABO+S△BPO=48，
（当OA=OB时，若BP∥OA，如图（6），作PF⊥x轴，
则∠AOC=∠PBF，∠ACO=∠PFB=90°，△AOC∽△PBF，
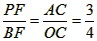，设BF=4m，PF=3m，
则点P的坐标为（4m-5，-3m），代入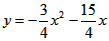
，解得m=
，
则点P的坐标为（1，-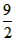
），
S梯形ABPO=S△ABO+S△BPO=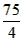
，
若OP∥AB（图略），
作PF⊥x轴，则∠ABC=∠POF，∠ACB=∠PFO=90°，△ABC∽△POF，
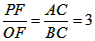，设点P的坐标为（-n，-3n），代入
，
解得n=9，则点P的坐标为（-9，-27），
S梯形AOPB=S△ABO+S△BPO=75。
