问题
解答题
已知二次函数y1=x2-2x-3及一次函数y2=x+m。
(1)求该二次函数图象的顶点坐标以及它与x轴的交点坐标;
(2)将该二次函数图象在x轴下方的部分沿x轴翻折到x轴上方,图象的其余部分不变,得到一个新图象,请你在图中画出这个新图象,并求出新图象与直线y2=x+m有三个不同公共点时m的值;
(3)当0≤x≤2时,函数y=y1+y2+(m-2)x+3的图象与x轴有两个不同公共点,求m的取值范围。
答案
解:(1)二次函数图象的顶点坐标为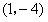
与x轴的交点坐标为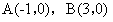 。
。
(2)①当直线位于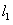 时,此时
时,此时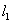 过点
过点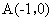
∴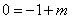 ,即
,即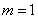
②当直线位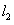 于时,此时
于时,此时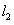 与函数
与函数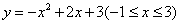 的图象有一个公共点
的图象有一个公共点
∴方程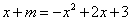 有一根
有一根
∴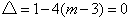 ,即
,即
当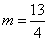 时,
时,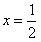 满足
满足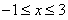
由①②知,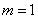 或
或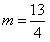 。
。
图像“略”。
(3)∵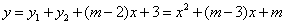
∵当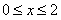 时,函数
时,函数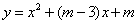 的图象与x轴有两个不同交点,
的图象与x轴有两个不同交点,
∴应同时满足下 * * 方面的条件:
①方程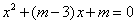 的判别式△=
的判别式△=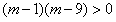
②抛物线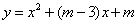 的对称轴满足
的对称轴满足
③当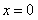 时,函数值
时,函数值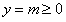
当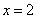 时,函数值
时,函数值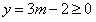
即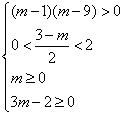
解得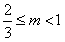
∴当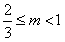 时,函数图像
时,函数图像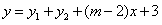 (
(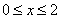 )的图象与轴有两个不同公共点。
)的图象与轴有两个不同公共点。
