问题
解答题
已知抛物线y=kx2-2kx+9-k（k为常数，k≠0），且当x＞0时，y＞1。
（1）求抛物线的顶点坐标；
（2）求k的取值范围；
（3）过动点P（0，n）作直线l⊥y轴，点O为坐标原点。
①当直线l与抛物线只有一个公共点时，求n关于k的函数关系式；
②当直线l与抛物线相交于A、B两点时，是否存在实数n，使得不论k在其取值范围内取任意值时，△AOB的面积为定值？如果存在，求出n的值；如果不存在，说明理由。
答案
解：（1）∵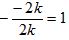
，
，
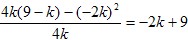∴抛物线的顶点坐标为（1，-2k+9）；
（2）依题意可得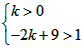
，解得0＜k＜4，即k的取值范围是0＜k＜4；
（3）①当直线l与抛物线只有一个公共点时，即直线l过抛物线的顶点，
由（1）得n关于k的函数关系式为n=-2k+9（0＜k＜4）；
②结论：存在实数n，使得△AOB的面积为定值，
理由：n=kx2-2kx+9-k，整理，得（x2-2x-1）k+（9-n）=0，
∵对于任意的k值，上式恒成立，
∴
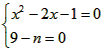，解得
，
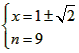∴当n=9时，对k在其取值范围内的任意值，抛物线的图象都通过点（1-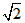
，9）和点（1+
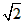，9），
即△AOB的底AB=2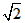
，高为9，因此△AOB的面积为定值9
。
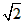