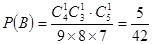①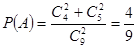

②

③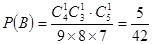

本试题主要是考查了排列组合在实际生活中的运用。

（1）第一问中，根据盒中放有的黑球和白球，其中黑球4个，白球5个. 从盒中同时摸出两个球，求两球颜色恰好相同，分为两种情况，然后相加得到。

（2）从盒中摸出一个球，放回后再摸出一个球，因为是又放回的摸球，因此每次摸球的时候都是9个球，那么两球颜色恰好不同的情况自然为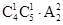，且有顺序。

（3）因为取到白球则停止摸球，求取到第三次时停止摸球，那么前两次取到为黑球，最后第一取到白球，的情况共有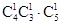，利用古典概型概率可得。

解：①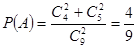

②

③