问题
解答题
现有编号为1，2，3，4，5的五个球和编号为1，2，3，4，5的五个盒子，将这五个球放入5个盒子内.
(1)若只有一个盒子空着，共有多少种投放方法？
(2)若没有一个盒子空着，但球的编号与盒子编号不全相同，有多少种投放方法？
（3）若每个盒子内投放一球，并且至少有两个球的编号与盒子编号是相同的，有多少种投放方法？
答案
解：（1）
（种） 。。。。。。。2分
（2）
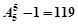（种） 。。。。。。。4分
（3）满足的情形：第一类，五个球的编号与盒子编号全相同的放法：1种
第二类，四个球的编号与盒子编号相同的放法：0种
第三类，三个球的编号与盒子编号相同的放法：10种
第四类，二个球的编号与盒子编号相同的放法：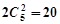
种
∴ 满足条件的放法数为： 1+10+20=31（种） 。。。。。。。8分
本试题主要是考查了组合数的运用。
（1）编号为1，2，3，4，5的五个球和编号为1，2，3，4，5的五个盒子，将这五个球放入5个盒子内.
若只有一个盒子空着，也就是将5个球放入4个盒子中，可知为
（2）若没有一个盒子空着，但球的编号与盒子编号不全相同，则可以云改用间接法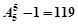得到
（3）满足的情形：第一类，五个球的编号与盒子编号全相同的放法：1种
第二类，四个球的编号与盒子编号相同的放法：0种
第三类，三个球的编号与盒子编号相同的放法：10种
第四类，二个球的编号与盒子编号相同的放法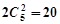：种
讨论得到。
