问题
解答题
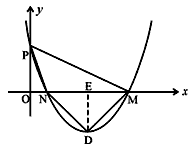
△ABC中，∠A，∠B，∠C的对边分别为a，b，c，抛物线y=x2-2ax+b2交x轴于两点M，N，交y轴于点P，其中M的坐标是（a+c，0）。
（1）求证：△ABC是直角三角形；
（2）若S△MNP=3S△NOP，①求cosC的值；②判断△ABC的三边长能否取一组适当的值，使三角形MND（D为抛物线的顶点）是等腰直角三角形？如能，请求出这组值；如不能，请说明理由。
答案
解：（1）证明：∵抛物线y=x2-2ax+b2经过点M（a+c，0），
∴（a+c）2-2a（a+c）+b2=0，
∴
，
∴
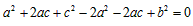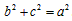
由勾股定理的逆定理得：△ABC为直角三角形；
（2）①如图所示；
∵S△MNP=3S△NOP，
∴MN=3ON即MO=4ON，
又M（a+c，0），
∴N（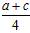
，0）
∴a+c，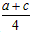
是方程x2-2ax+b2=0的两根，
∴（a+c）+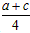
=2a，
∴c=
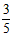a，
由（1）知：在△ABC中，∠A=90°，
由勾股定理得b=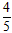
a，
∴cosC=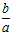
=
；
②能；
由（1）知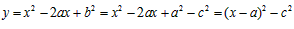
，
∴顶点D（a，-c2），
过D作DE⊥x轴于点E，则NE=EM，DN=DM
要使△MND为等腰直角三角形，
只须ED=
MN=EM，
∵M（a+c，0），D（a，-c2），
∴DE=c2，EM=c，
∴c2=c，又c＞0，
∴c=1，
由于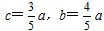
，
∴
，
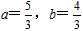当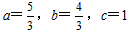
时，△MNP为等腰直角三角形。
