问题
填空题
在斜二测投影下，四边形ABCD是下底角为45°的等腰梯形，其下底长为5，一腰长为
|
答案
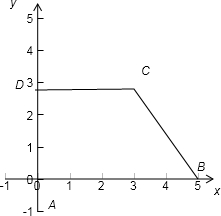
作DE⊥AB于E，CF⊥AB于F，则AE=BF=ADcos45°=1，
∴CD=EF=3．将原图复原（如图），
则原四边形应为直角梯形，∠A=90°，AB=5，CD=3，AD=2
，2
∴S四边形ABCD=
?（5+3）?21 2
=82
．2
故答案为：8
．2
搜题请搜索小程序“爱下问搜题”