参考答案：C

解析：[要点解析] 解答方法(1)
解答步骤如下：
(1)根据图9-14画出能够放在同一箱的药品连线图，如图9-15所示。图中的各节点表示各种化学药品，节点之间的连线(边)表示这2个节点所代表的药品可以装在同一箱中(即图9-14中留空的格子)。

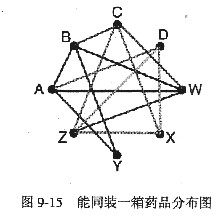
(2)8种化学药品不计装箱顺序的情况下，同装3箱的组合方案有(1、1、6)、(1、2、5)、(1、3、4)、(2、2、4)、 (2、3、3)。
(3)可先讨论(2、3、3)的组合方案。
①先找出图9一15中3种化学药品可以同装一箱的组合，即图9-15中的所有的三角形(处于3条边上的顶点刚好“两两相容”)。这样的组合共有6种，分别是：ABY、ABw、BCW、CXZ、CWZ、DXZ。
②找出这6组数据中，所有的不相交的数据组。
ABY，CXZ：剩下D、W，而D、W在图9-15中无连接的边，即不能同装一箱，因此满足(ABY，CXZ)组合时需要4个箱子，即不是同装3箱的组合方案。
ABY，CWZ：剩下D、X，在图9-15中D、X有连接的边，即可以同装一箱，因此需要3个箱子，是同装3箱的一种组合方案。
ABY，DXZ：剩下C、W，C、W可以同装一箱，这是同装3箱的一种组合方案。
ABw，CXZ：剩下D、Y，而D、Y不能同装一箱，因此需要4个箱子。
ABW，DXZ：剩下C、Y，而C、Y不能同装一箱，因此需要4个箱子。
BCW，DXZ：剩下A、Y，A、Y可以同装一箱，这是同装3箱的一种组合方案。
至此，不计装箱顺序的情况下，(2、3、3)的方案有3种组合形式。
(4)接着可讨论是否存在4种化学药品可以同装一箱的组合。在图9-15中可以找到ABCW的4边形，但AC之间没有连接的边，因此ABCW不能同装一箱。
同理，虽然存在BYAW、BWZC、CZDX等4边形，但不能实现组内化学药品“两两相容”。
由此可知，含有4种化学药品可以同装一箱的组合方案(1、3、4)和(2、2、4)是不成立的。
当然，此证明还可从3种化学药品可以同装一箱的组合的基础上进一步讨论。找出ABY、ABW、BCW、CXZ、CWZ、DXZ组合中分别有两种相同化学药品的情况。
①对于ABY、ABW，虽然AB可以同装一箱，但YW不能同装一箱；
②对于ABw、BCW，虽然BW可以同装一箱，但AC不能同装一箱；
③对于BCW、CWZ，虽然CW可以同装一箱，但BZ不能同装一箱；
④对于CXZ、CWZ，虽然CZ可以同装一箱，但XW不能同装一箱；
⑤对于CXZ、DXZ，虽然XZ可以同装一箱，但CD不能同装一箱。
至此，不存在4种化学药品可以同装一箱的组合，即任何4种药品都不能同时放在一个箱子中。
(5)进一步推理可知，既然找不到4种化学药品可以同装一箱的组合，那么也就不存在5种或6种化学药品可以同装一箱的组合。因此，组合方案(1、2、5)和(1、1、6)是不成立的。
(6)由以上分析可知，运输这8种化学药品至少需要装3个箱子，实现这种最少箱数的装箱方案(不计装箱顺序)可有3个，即(1)空的正确答案为选项B，(2)空的正确答案为选项C。
解答方法(2)
依题意可得到图9-16，图中的节点表示化学药品，边表示相应的两种药品不能同装一箱，即不能放在一起(图9-14中带“×”的格子)。

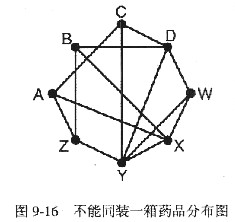
图9-16中与节点Y相连的边数最多，因此可从节点Y入手进行分析。
装箱方案1：Y与A、Y与B无相互连接的边，可将这3种化学药品同装一箱。对于剩余的C、D、w、X、z化学药品中，可将C、W、X、Z这4种化学药品同装一箱，D单独放在一个箱子中，即(A、B、Y)、(C、W、X、Z)和(D)。
同理，可得到装箱方案2：(A、B、Y)、(C、W、Z)和(D、X)；装箱方案3：(A、B、Y)、(C、W、X)、(D、Z)；装箱方案4：(B、Y)、(C、W、X、Z)、(A、D)。
同时可证明不存在4种(或5种，或6种)化学药品可以同装一箱的组合。