问题
解答题
一家用电器开发公司研制出一种新型电子产品,每件的生产成本为18元,按定价40元出售,每月可销售20万件,为了增加销量,公司决定采取降价的办法,经市场调研,每降价1元,月销售量可增加2万件。(1)求出月销售量y(万件)与销售单价x(元)之间的函数关系式(不必写x的取值范围);
(2)求出月销售利润z(万元)(利润=售价-成本价)与销售单价x(元)之间的函数关系式(不必写x的取值范围);
(3)请你通过(2)中的函数关系式及其大致图象帮助公司确定产品的销售单价范围,使月销售利润不低于480万元。
答案
解:(1)y=20+2(40-x)=-2x+100,
∴y与x的函数关系式为y=-2x+100;
(2)z=(x-18)y=(x-18)(-2x+100)=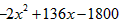 ,
,
∴z与x的函数关系式为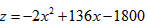 ;
;
(3)令z=480,得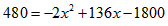 ,整理得
,整理得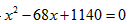 ,
,
解得,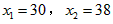 ,
,
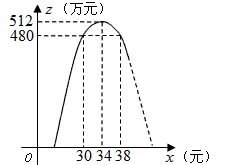
将二次函数解析式变形为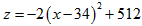 画出大致图象如图,
画出大致图象如图,
由图象可知,要使月销售利润不低于480万元,产品的销售单价应在30元到38元之间(即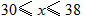 )。
)。