问题
填空题
已知三棱锥SABC的所有顶点都在球O的球面上，△ABC是边长为1的正三角形，SC为球O的直径，且SC＝2，则此三棱锥的体积为________．
答案
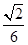
在Rt△ASC中，AC＝1，∠SAC＝90°，SC＝2，所以SA＝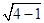
＝
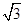.同理，SB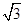＝.过A点作SC的垂线交SC于D点，连接DB，因为△SAC≌△SBC，故BD⊥SC，AD＝BD，故SC⊥平面ABD，且△ABD为等腰三角形．因为∠ASC＝30°，故AD＝
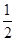SA＝
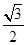，则△ABD的面积为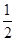×1×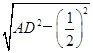
＝
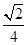，则三棱锥S-ABC的体积为
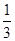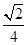××2＝