问题
解答题
已知抛物线y=ax2+bx+c与y=2x2开口方向相反，形状相同，顶点坐标为（3，5）。
（1）求抛物线的关系式；
（2）求抛物线与x轴、y轴交点。
答案
解：（1）∵抛物线y=ax2+bx+c与y=2x2形状相同，开口方向相反，
∴a=-2
又∵抛物线顶点为（3，5），
∴y=-2（x-3）2+5=-2x2+12x-13
（2）当x=0时，y=-13，即抛物线与y轴交点为（0，-13）；
当y=0时，有x1=3+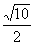
，x2=3-
，
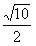即抛物线与x轴交点坐标为（3+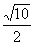
，0），（3-
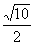，0）。