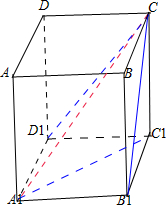
如图，把已知几何体长为

7

的棱看做某一个长方体的对角线，设长方体的对角线A₁C=

7

，则它的正视图的投影长为D1C=

6

，侧视图的投影长为B₁C=a，俯视图投影长为A₁C=b

，

则a2+b2+(

6

)2=2×(

7

)2，即a²+b²=8．

∵a²+b²≥2ab，∴2（a²+b²）≥（a+b）²，∴

a+b

2

≤

a2+b2 2

=2，当且仅当“a=b=2”时取等号．

∴a+b≤4，即a+b的最大值为4．