问题
解答题
已知函数y=2x和抛物线y=ax2+3相交于点(2,b).
(1)求a,b的值;
(2)若函数y=2x的图象上纵坐标为2的点为A,抛物线y=ax2+3的顶点为B,求S△AOB.
答案
解:(1)∵点(2,b)在直线y=2x上,
∴b=4,
又∵(2,b)即(2,4)在抛物线y=ax2+3上,
∴4a+3=4,
∴a= ;
;
(2)在y=2x中,令y=2,则x=1,
∴A(1,2),
则抛物线y= x2+3的顶点B为x=﹣
x2+3的顶点B为x=﹣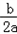 =﹣
=﹣ =0,y=
=0,y= =
=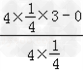 =3,
=3,
故顶点B(0,3),
∴S△AOB= OB·|xA|=
OB·|xA|= ×3×1=
×3×1= .
.
