问题
填空题
某几何体的一条棱长为
|
答案
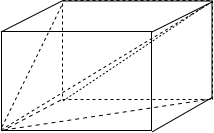
由棱和它在三视图中的投影扩展为长方体，
三视图中的三个投影，是三个面对角线，
则设长方体的三度：x、y、z，
所以x2+y2+z2=7，x2+y2=a2，y2+z2=b2，
x2+z2=6可得a2+b2=8
∵（a+b）2≤2（a2+b2）
a+b≤4
∴a+b的最大值为：4
故答案为：4
搜题请搜索小程序“爱下问搜题”
某几何体的一条棱长为
|
由棱和它在三视图中的投影扩展为长方体，
三视图中的三个投影，是三个面对角线，
则设长方体的三度：x、y、z，
所以x2+y2+z2=7，x2+y2=a2，y2+z2=b2，
x2+z2=6可得a2+b2=8
∵（a+b）2≤2（a2+b2）
a+b≤4
∴a+b的最大值为：4
故答案为：4