问题
选择题
有5盆互不相同的玫瑰花，其中黄玫瑰2盆、白玫瑰2盆、红玫瑰1盆，现把它们摆放成一排，要求2盆白玫瑰不能相邻，则这5盆玫瑰花的不同摆放种数是（ ）
A．120
B．72
C．12
D．36
答案
答案：B
题目分析：第一步：先摆黄玫瑰和红玫瑰，摆法有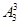
种；第二步：再摆白玫瑰，由于黄玫瑰和红玫瑰之间有4个位，则有摆法
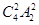种，所以这5盆玫瑰花的不同摆放种数是
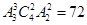种。故选B。
点评：关于排列和组合的题目，常用到捆绑法和插位法。捆绑法是将一些对象看作一个对象进行排列；插位法是将一些对象进行排列后，再对剩下的对象进行排列。本题用到插位法。