问题
问答题
某一旅游景区,建有一山坡滑草运动场.该山坡可看成有一定倾角的斜面,一名游客与滑草装置总质量m=80kg,他从静止开始匀加速下滑,t=5s时滑至底端.已知斜面和水平面动摩擦因数相同,游客在整个运动过程中速率v与时间t的关系如图所示(不计空气阻力,g取10m/s2,)求:
(1)滑草装置与草皮间的动摩擦因数μ;
(2)斜面的倾角θ;
(3)通过计算证明游客从顶端滑至底端的过程满足动能定理.
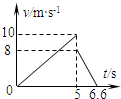
答案
(1)游客和滑草装置整体在水平草皮上作匀减速运动时,由v-t图加速度大小为:
a1=5m/s2=μg,
μ=0.5
(2)游客和滑草装置整体在斜面上作匀加速运动时,由:gsinθ-μgcosθ=2m/s2,
结合sin2θ+cos2θ=1,
则sinθ=0.6,即θ=37°;
(3)游客在此过程中,
重力做功:WG=mgxsinθ=80×10×25×0.6=12000J,
斜面的摩擦力做功:Wf=-μmgxcosθ=-8000 J,
动能的增量△EK=
m1 2
-v 2t
m1 2
=4000-0=4000Jv 20
则合外力的功W合=WG+Wf=4000 J,
W合=△EK即可证明.
答:(1)滑草装置与草皮间的动摩擦因数μ为0.5;
(2)斜面的倾角θ等于37°;
(3)W合=△EK即可证明,游客从顶端滑至底端的过程满足动能定理.
