某电子厂商投产一种新型电子厂品,每件制造成本为18 元,试销过程中发现,每月销售量y (万件)与销售单价x (元)之间的关系可以近似地看作一次函数y= ﹣2x+100 .(利润= 售价﹣制造成本)
(1 )写出每月的利润z (万元)与销售单价x (元)之间的函数关系式;
(2 )当销售单价为多少元时,厂商每月能获得3502 万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3 )根据相关部门规定,这种电子产品的销售单价不能高于32 元,如果厂商要获得每月不低于350 万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
解:(1 )z= (x -18 )y= (x -18 )(-2x+100 )= -2x2+136x-1800 ,
∴z 与x 之间的函数解析式为z= -2x2+136x-1800 ;
(2 )由z=350 ,得350= -2x2+136x -1800 , 解这个方程得x1=25 ,x2=43
所以,销售单价定为25 元或43 元,
将z =-2x2+136x-1800 配方,得z=-2 (x-34 )2+512 ,
因此,当销售单价为34 元时,每月能获得最大利润,最大利润是512 万元;
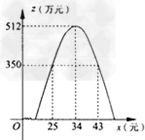
(3 )结合(2 )及函数z=-2x2+136x ﹣1800 的图象(如图所示)可知,
当25≤x ≤43时z ≥350 ,
又由限价32 元,得25 ≤x ≤32 ,
根据一次函数的性质,得y=-2x+100 中y 随x 的增大而减小,
∴当x=32 时,每月制造成本最低
最低成本是18 ×(-2 ×32+100 )=648 (万元),
因此,所求每月最低制造成本为648 万元.