问题
解答题
已知函数y=x2+bx+c过点A（2，2），B（5，2）。
（1）求b、c的值；
（2）求这个函数的图象与x轴的交点C的坐标；
（3）求S△ABC的值。
答案
解：（1）把A（2，2），B（5，2）分别代入y=x2+bx+c，
可得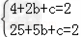
，
解得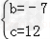
；
（2）由b=-7，c=12，知y=x2-7x+12
令y=0，得x2-7x+12=0，
∴x=3或x=4，
∴C（3，0）或C（4，0）；
（3）∵A（2，2）B（5，2）
∴AB=|2-5|=3，且△ABC的AB边上的高h=2，
∴S△ABC=
AB·h=
×3×2=3。