问题
解答题
已知函数f(x)=ax3+x2-ax,其中a,x∈R.
( I)当a=1时,求函数f(x)的单调递减区间;
(Ⅱ)若函数f(x)在区间(1,2)上不是单调函数,求实数a的取值范围;
(Ⅲ)若x∈[0,3]时,函数f(x)在x=0处取得最小值,求实数a的取值范围.
答案
(Ⅰ)当a=1时,f(x)=x3+x2-x.f'(x)=3x2+2x-1,
由f'(x)<0,即3x2+2x-1<0,得-1<x<
,1 3
即当a=1时,函数f(x)的单调递减区间为(-1,
).1 3
(Ⅱ)由f'(x)=3ax2+2x-a.
要使函数f(x)在区间(1,2)上不是单调函数,
则方程f'(x)=0在区间(1,2)内有不重复的零点,
而△=4+12a2>0,由3ax2+2x-a=0,得a(3x2-1)=-2x
∵x∈(1,2),∴(3x2-1)≠0,∴a=-
;2x 3x2-1
令u=-
(x∈(1,2)),则u=-2x 3x2-1
,2 3x- 1 x
∴u=-
在区间(1,2)上是单调递增函数,其值域为(-1,-2x 3x2-1
),4 11
故a的取值范围是(-1,-
).4 11
(Ⅲ)由题意可知,当x∈[0,3]时,f(x)≥f(0)=0恒成立,
即x∈[0,3]时,ax2+x-a≥0恒成立.
记h(x)=ax2+x-a
当a=0时,h(x)=x≥0在x∈[0,3]时恒成立,符合题意;
当a>0时,由于h(0)=-a<0,则不符合题意;
当a<0时,由于h(0)=-a>0,则只需h(3)=8a+3≥0,得a≥-
,3 8
即-
≤a<0.3 8
综上,-
≤a≤0.3 8

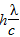 ,m=0
,m=0 ,m=
,m=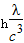
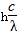 ,m=0
,m=0 ,m=
,m=